Making the Master System a Master of Speech
The Intellivision Voice Synthesis Module was released in 1982, giving the 16-bit console the power of speech. But unfortunately, most other consoles weren’t quite as lucky. Sure, some systems, like the PC Engine CD and Nintendo Famicom, have the ability to play samples directly, so at least they can do pre-recorded speech. But the Sega Master System can’t even do that. So how do we manage?
You know it’s possible
Have you ever played Alex Kidd: The Lost Stars? If not, immediately go out right now and buy it (the post not sponsored by Sega) and put it in your Sega(tm) Master System. You’ll hear a miracle: the console speaks. (Possibly a bit too quietly as my Master System is having a bad day)
Now put the game aside to keep reading this post. Those stars are already lost, what’s a little longer?
What does the Sega say?
The Sega Master System, as I noted in my overview post, uses the SN76489A sound chip (often just called the “PSG”, for Programmable Sound Generator, though that’s a generic term used for multiple chips). Well, a Sega clone of it, anyway. This is a 4-voice sound chip, used here to play the Space Harrier theme in Space Harrier 3-D. (This one’s loud)
What are those four voices?
- 3 square wave channels
- 1 noise channel
You can also sacrifice one of the three square waves to get more noise frequencies, but that’s not important right now. What is important to note is that none of these seem able to play arbitrary sounds, like “FIND THE MIRACLE BALL”. (Or is it “I’M THE MIRACLE BALL?”) Square wave tones and noise can do a lot, but they can’t talk to you.
But then again, what is a sample?
All the world’s a DAC
Here’s a computer voice saying “warning”, generated by using the say command in Mac OS. My game is a shoot ‘em up, and I want to have an overly dramatic pre-boss intro, because those are fun. Have a gratuitous screenshot of DoDonPachi DaiOuJou Tamashii.

But of course, if you look at the file in a hex editor, you’ll never see the word “warning” (unless there’s a really strange coincidence). What do you need to do with seven bytes when 19 kiB will do? The word “warning” is encoded as a waveform.

The main property of this wave that makes it a wave is that it is single-valued; it has one value at any given point in time. When your computer plays it back, it therefore is constantly moving its speaker, and the displacement is the wave. More or less, anyway.
So your computer can do this because it has a DAC, a digital-to-analog converter. We saw a DAC in the Vectrex article; you put an 8-bit value of bits on one side, and get an analog voltage on the other. So if you wanted to output this wave, you could take all its values, and carefully put them out on the DAC.
But the thing is, the definition of a DAC is pretty broad. An on-and-off switch? That’s a DAC. And you can turn the sound chip off and on on pretty much anything with one.
Imagine being able to set the SN76489 to just output a constant voltage– a wave with zero frequency. Your speaker wouldn’t move. Now you turn it off. The speaker moves. This becomes a lot like the Apple ][ audio without a sound card. Extremely CPU intensive. But if you’re fast enough, you can get the system to talk. You can even get it to say “find the miracle ball”. That’s what Alex Kidd: The Lost Stars does.
Let’s take our 22.050kHz signal, and amplify it to full settings. This will cause massive clipping, but the “warning” is still audible, if barely. (This is a heavily amplified signal, so set your system volume accordingly)
Now, “one-bit” audio like this can actually be very good quality. But you trade frequency for speed. Alex Kidd: The Lost Stars uses 17.3kHz samples (thanks to Maxim at SMS Power) for the section shown. My “warning” is 22.050kHz, but probably sounds worse because of the lazy way I created it. To look at the real 1-bit DACs, the professional-quality “Super Audio CD” format uses a 2.82 MHz 1-bit DAC stream.
No matter what you do to get more quality, the biggest tradeoff of this method will always remain: it uses, more or less, 100% of the CPU time. Even the frame interrupts are painful. A 60Hz (or 50Hz, if you’re into that sort of thing) tone is definitely audible, so you’ll need to disable them.
More or less, playing a sample on the Sega Master System means you use 100% of your CPU time. And I did know that going in; hence why I want to use it for a warning screen, not for, just randomly guessing, a punch sound in an action-game.
Yeah, yeah, keep showing off with your fancy delta-modulation sample channel…
More skills
So if we want to play samples in higher quality, what are our options? We could try to increase the frequency of 1-bit samples, but remember that we’re feeding this with a 4MHz Z80, and just loading a constant value into a register and then outputting on or off to a single PSG channel will cost 15 cycles. That ignores the time taken to read the sample from memory or to do a loop.
There is, however, an alternative. Each of the three square-wave channels (the noise isn’t really useful for this) of the PSG has a 4-bit volume control. We can even go beyond 4-bits: if we control the three channels in quick succession, we could use this to create a variety of volume levels. (This does not create 12 bits worth of output, though, as some values will create the same volume)
This is the method taken by the 1991 port of Populous, released only in Europe and Brazil. It’s a bit quiet. Unfortunately, this method will always be less loud than the 1-bit approach.
Well it’s a Europe exclusive, so if you’re curious how 50Hz mode impacts things. Spoilers: This is all CPU-timed, so the video frame rate doesn’t actually matter as much.
Populous uses three lookup tables, one for each channel. Here’s my take on the concept, in Z80 Assembly. I’ve tried to comment it heavily, but if you don’t want to try to read assembly today, it’s fine to skip the block. It’s just the same concept described above.
playSample:
call PSGStop ; part of PSGLib library, turns off any sound playing
di ; disable interrupts
; set tone to 0
ld a, %10000000 ; ch 0 tone 0
out (psg),a ; send to PSG
xor a ; zero out the rest of the tone
out (psg),a ; send to the PSG
ld a, %10100000 ; ch 1
out (psg),a
xor a ; xor a is equivalent to ld a,0, but faster
out (psg),a
ld a, %11000000 ; ch 2
out (psg),a
xor a
out (psg),a
dec hl ; because the loop starts with an increment
@main_sample_loop:
inc hl
ld a, (hl)
push hl
ld h,hibyte(sample_table) ; sample table stored in 256-byte aligned memory
ld l,a ; so the lower byte of the table always starts at 00
ld a,(hl)
out (psg),a ; changing PSG volume can be done with only one byte
inc h ; increase the high byte of our address; the next table
ld a,(hl)
out (psg),a
inc h
ld a,(hl)
out (psg),a
pop hl
ld e, d ; Delay
-: dec e ; to ensure the frequency rate matches the desired
jr nz, -; rather than going as fast as possible
dec bc ; Decrement byte counter
ld a, b
or c ; b OR c will only be zero if bc is zero
jr nz, @main_sample_loop ; Loop until we run out of bytes
@done:
call PSGStop ; in case we left any dangling sounds
ei ; turn interrupts back on
ret
So that’s fine and dandy. The delay allows samples of different frequencies; the correct way to determine the mapping of sample to frequency would be to count the cycles in our loop. But instead I just guessed and tried different values until it sounded okay.
What does it sound like?
A little bit worse for wear, the sound is a bit softened. (I did drop it to 16kHz but that shouldn’t be a huge impact) But the biggest issue is one that probably isn’t clear from this capture, since I amplified it, but might have been obvious in the Populous clip above (since I didn’t): the sample is very quiet.
What’s the deal with that sound table?
I kind of glossed over the sound table. What does it look like? Well, the one that was, uh, borrowed from Populous looks like as follows:
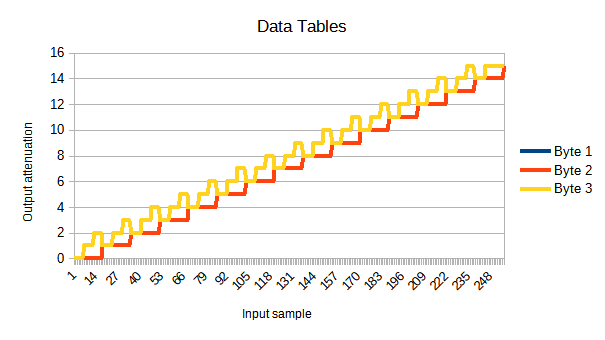
I’m not sure what’s going on with channel 3 there; the tables for bytes 1 and 2 are identical; both being used just gives you some increase in volume, which as you can probably tell so far, we desperately need.
But this graph doesn’t tell you the whole story. See, this isn’t a graph of sample vs. output volume, it’s a graph of what the SN76489A calls attenuation. And attenuation is not volume. In fact, as the name suggests, it’s the opposite of volume. No attenuation means the full output of the chip occurs, and full attenuation means silence. Plus, it’s not linear, but logarithmic; the SN76489A acts in the realm of decibels.
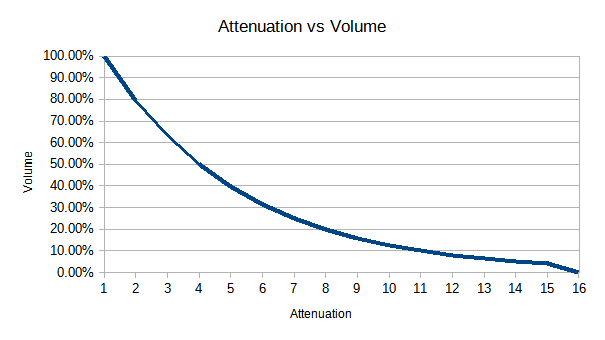
So now we can see one of the reasons the sample is so quiet– most of the attenuation space is taken up in low volume areas.
Can we do better?
So a fun thing here is that I don’t actually know if we can do better right now; I’m typing this post while I work on it. Of course, I could delete this paragraph if it ends up making me look bad. Not like this is a livestreamed blog, however that would work.
So first off I want to know all the possible volumes. You can imagine summing the three channels together to determine the output; I’m not sure that’s quite right, but it’s probably good enough. I generated a data table in python:
# taken from https://www.smspower.org/Development/SN76489#Volumeattenuation
volume_table_16bit = [
32767, 26028, 20675, 16422, 13045, 10362, 8231, 6568,
5193, 4125, 3277, 2603, 2067, 1642, 1304, 0
]
def generate_three_volumes():
values = []
for i in range(0,16):
for j in range(0,16):
for k in range(0,16):
volume = (
volume_table_16bit[i] +
volume_table_16bit[j] +
volume_table_16bit[k])
values.append({
"volume": volume,
"ch1": i,
"ch2": j,
"ch3": k
})
return values
This just sums together all the possible values. There are 4096 possible combinations of the three channels, but only 813 unique ones. Even fewer will be worth caring about for our 256 linear samples.
This function gives me volumes in the range between 98301 (32767 times 3) and 0. Which is fine. Here’s a new table, normalized to 100% volume.
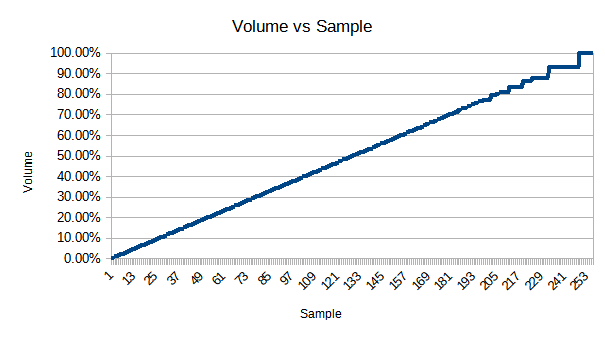
You can see that now it’s linear. However, it’s also now a bit clipped at the start and end, because of the combination of the three channels. I’m hoping this won’t matter. It does show why you have to make a quality sacrifice to get louder here.
Something matters, that’s for sure
Let’s listen to the two tracks side by side. Old first, then with the new table. (I’ve amplified these)
Well that’s surprising! It did sound better in the MEKA emulator, but on the Sega Master System 2 (the one from this post), there’s a lot of noise. Why is that? Well, if I look at the signal in Audacity, it’s definitely jaggedier.
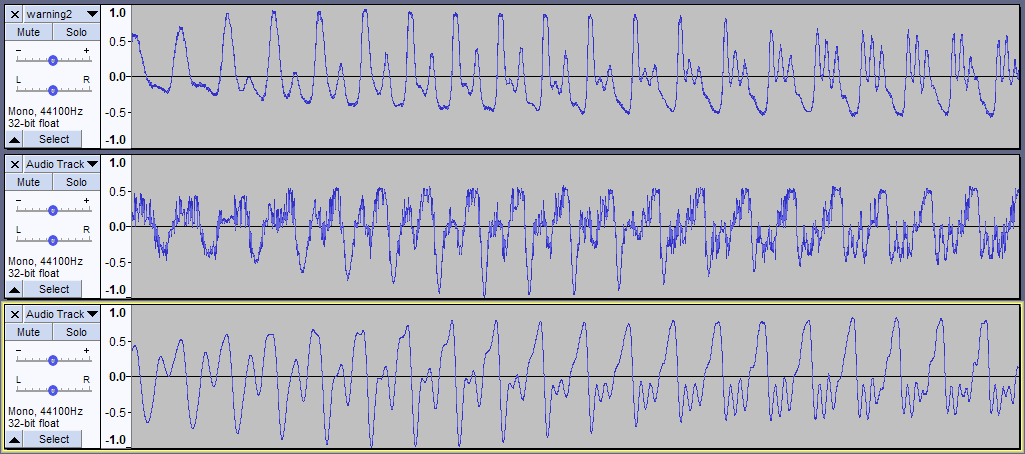
I included the original WAV file for comparison, just so you can see how with the new table we no longer have inverted the signal. So we fixed that problem, at least.
So I tried a few things here. For example, I disabled channel 3, since it had the weird behavior above, but it didn’t get rid of the noise. So what’s the issue? Let’s take a look at our tables. We’ll see it pretty quickly.
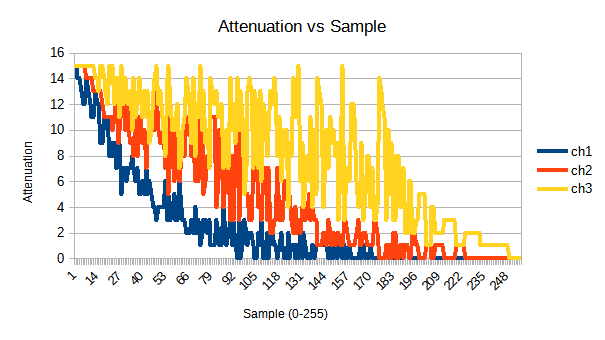
So even though the volume vs. sample graph is nice and smooth, our graph for each channel is very chaotic. Remember when I mentioned there were a lot of ways to get each possible volume? That’s what happens when you just go through all the possible values and pick the closest.
Why does this matter? Let’s look at our loop code, specifically, where we output the bytes to the PSG. But here, I’ve included the cycles of each. (The Z80 on the Master System runs at just about 3.5MHz)
out (psg),a
inc h ; 4 cycles
ld a,(hl) ; 7 cycles
out (psg),a ; 11 cycles
inc h ; 4 cycles
ld a,(hl) ; 7 cycles
out (psg),a ; 11 cycles
Notice that between the first output to the PSG register (that’s what out (psg),a means), and the last one, there are 22 cycles in which one channel is updated but the other two aren’t. Sure, that’s only a very short amount of time (~6,250 ns). But this is happening on every cycle.
If the “in-between” state is close to the states around it, that probably won’t matter much, as it doesn’t seem to for Populous’s linear table. But for my chaotic table, those intermediate states are putting out a lot of repetitive garbage on every byte of the sample. Repetitive garbage is also known as noise.
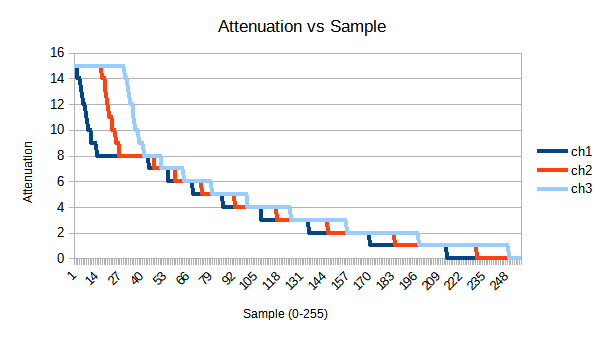
So how do we solve this? We basically want to make each channel monotonic. This just means that it always increases or decreases, rather than going all over the place.
I decided to do this in a simple way; starting at index 0, all the channels will have full attenuation. Then, at each step, I see if bringing down the attenuation of channel 1 will get closer to the volume. If not, I go to channel 2 and try that. Then channel 3. This gives a graph like below:
This is nice in theory, but what does it do to our total volume? I haven’t bothered to normalize them, but here it is compared to our last data.
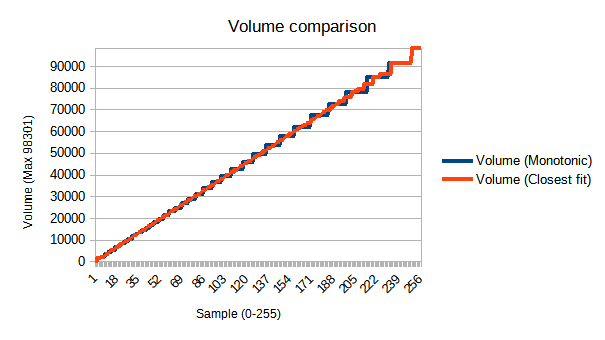
As you can see, our new volumes are noticeably more jagged. This is because our monotonicity requirement has dramatically limited the number of possible values we can get at any given step. Still, is it good enough?
Let’s take a listen
So I’d call this a small success. It’s definitely a big improvement over the second, but the improvement over the first is less so; it may even be noisier. (This capture isn’t the best; my Master System 2 doesn’t output a very loud signal) It’s definitely a bit louder (from waveform analysis) and maybe a bit higher quality, even.
I have to wonder now if the Populous data tables are inverted deliberately, in an attempt to compensate for the non-linearity of the attenuation table, without having to go through all the calculation.
Still, enough to be happy with, I’d say. What you don’t see in these posts, of course, are the intermediate tests, that didn’t make a difference or even made things worse. Even if you skim the technical details, though, I hope it was an interesting journey!
The journey hasn’t ended yet, of course. And a step on that journey might involve making better videos…
Don’t blame me, I’m from the future
You might wonder, why didn’t Populous take into account the characteristics of the PSG I mentioned? Let’s add it to our graph.
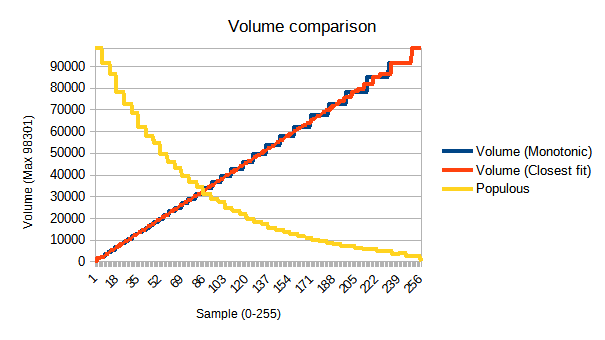
Well, I have a large number of advantages they didn’t. That includes:
- Modern, reverse-engineered documentation on the PSG– the Sega docs say nothing about sample playback
- Modern debugging emulators like MEKA that can both run a game in real time and easily step through it
- Modern flash carts that can quickly load new games (though I’m not sure about the Master System devkits of the time, so this might be a wash– anything involving burning EEPROMs, though, would be much slower)
- Modern programming languages like Python– Python came out in 1991, the same year as Populous, but wouldn’t reach its modern flexibility for a bit. (And this isn’t to mention the computing power I have that can run it fast!)
Finally, and probably most importantly of all, is that I have no deadlines or expectations bearing down. It doesn’t matter if I never finish this; as for Populous, though, delays cost the developers real money. They got the cool voice gimmick and moved on to the next task that needed work, and who can blame them? The difference isn’t really that great.
